Accurate Pi Theory
Accurate Pi Theory states that if one squares the outside of a circle that is made of rope/string. Then, stretch out the rope to find circumference then one may accurately solve for Pi.
By: Michael G. Strain Jr.
After performing the calculations, I found Pi to be 3.125.
Tips for solving for Pi with Accurate Pi Theory:
Make sure the string is level around the circle so that it is parallel to the table.
Make sure to square the circle and account for the width of the rope by including the width of the rope in the calculation of the diameter.
Make sure to not over stretch the string but to keep light even tension on the string.
Use premeasured no stretch string fishing wire or braid sewing thread even (should reduce stretch) or premeasured wax coated thread.
Consider whiteout for the no fishing wire as a marker and a felt tip pen for cloth.
Use an outside caliper for larger circles as these are much more inexpensive.
Straight Line Circle Theory
Straight Line Circle Theory states that the reason a line ought not be used inside the circle for radius is because a line is straight and has square edges and the arc of a circle is round. Thus, when the radius of a circle is measured as a line in the center of the circle, the line does not sit flush against the arc of a circle. Because the line does not sit flush against the arc of the circle the radius cannot be accurately measured. Therefore, in theory a line in the center of a circle cannot accurately measure the radius of a circle.
By: Michael G. Strain Jr.
The ebook has further explanations on the different theories.
Rope Circumference Theory
Rope Circumference Theory states that measuring circumference with a rope or tape on the outside of the circle is not an accurate method of measuring circumference because the rope/tape makes a bigger circle than the one being measured. A smaller circle has a smaller circumference than a bigger circle. Thus the thickness of the rope/tape itself does, in theory, inherently increase the measurement of circumference. Thus a rope or tape does not accurately measure circumference.
By: Michael G. Strain Jr.
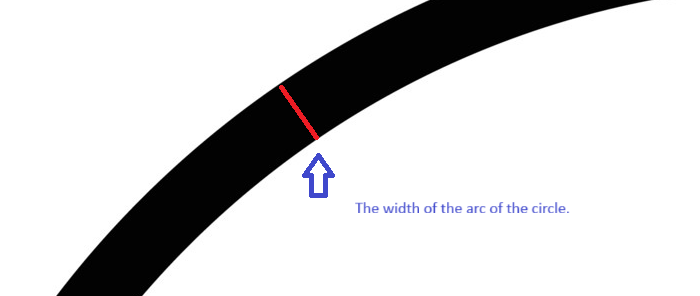
Arc Theory
Arc Theory states that the thickness of the arc of the circle will change measurement of the diameter. The thickness of the arc of a circle theoretically makes the old method even more inaccurate because it is not accounted for with certain or most circles. Thus, in theory the circle must be filled in before one measures the diameter in order to provide a more accurate measurement. The width of the arc of the circle would shorten the diameter even. For further clarification of the width of the arc see the image to the right.
By: Michael G. Strain Jr.